Linear Algebra

Information on this page is taken from the Imperial College London's course.

Overview

Linear algebra is the study of vectors, vector spaces, and mapping between vector spaces. Linear algebra emerged from the study of linear equations an the realization that these could be solved with vectors and matrices.

Vectors

In physics, a vector is often used to describe movement in physical space. In data science, a vector is often a list of attributes about an object.

Vector Operations

Addition and Multiplication

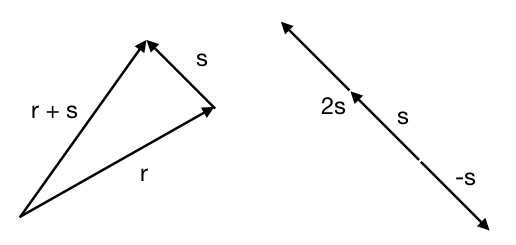
vector-operations.png

Note that addition is communicative (\(r + s = s + r\)) and associative (\((r + s) + t = r + (s + t)\)).

Addition happens by components:

\begin{equation} \begin{bmatrix} 1 \\ 2 \end{bmatrix} + \begin{bmatrix} 3 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \end{bmatrix} \end{equation}

Length

A vector's length (also known as modulus or size) is the sum of the squares of its components. With two components this is

\begin{equation} |r| = \sqrt{a^2 + b^2} \end{equation}

Think of vectors geometrically for a second. Notice that this length operation is calculating the hypotenuse (\(c = \sqrt{a^2 + b^2}\)).

Dot Product

The dot product (also known as the inner product) is an operation that takes two vectors and produces a scalar.

\begin{equation} r \cdot s = r_i s_i + r_j s_j \end{equation}

The dot product is commutative (\(r \cdot s = s \cdot r\)), distributive (\(r \cdot (s + t) = r \cdot s + r \cdot t\)), and associative over scalar multiplication (\(r \cdot (as) = a(r \cdot s)\) where \(a\) is a scalar).

Interestingly, \(r \cdot r = |r|^2\).

The cosine rule tells us that

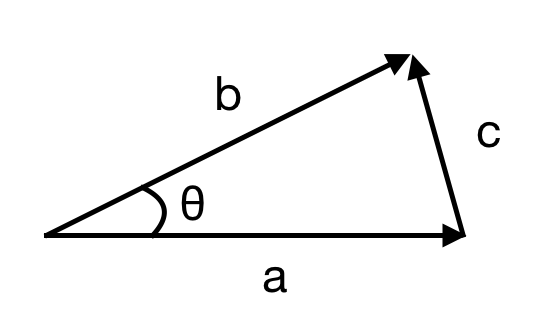
cosine-rule.png

\begin{equation} c^2 = a^2 + b^2 - 2ab\cos\theta \end{equation}

If we substitute these values for vector lengths, we get

\begin{equation} |r - s|^2 = |r|^2 + |s|^2 - 2|r||s|\cos\theta \end{equation}

This equation can then be simplified to

\begin{equation} r \cdot s = |r||s|\cos\theta \end{equation}

This equation then tells us some interesting facts about the dot product. Since we know that \(\cos90 = 0\), a dot product of 0 must mean that the two vectors are orthogonal. Since \(\cos0 = 1\), a positive dot product means that the vectors are going the same way. Lastly, since \(\cos180 = -1\), a negative answer for the dot product means that the lines are going in more or less opposite directions.

TODO Projection

Vectors and Data Science

Let's say that we have a distribution. We'd like to find the normal distribution that best fits the data. Here's an example:

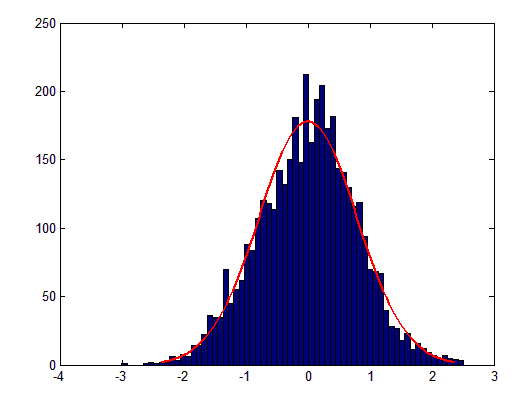
distribution-fit.png

The normal distribution has two parameters: \(\sigma\) and \(\mu\). We need to find the best values for these two parameters.

Here's an example of a bad \(\sigma\) and \(\mu\).

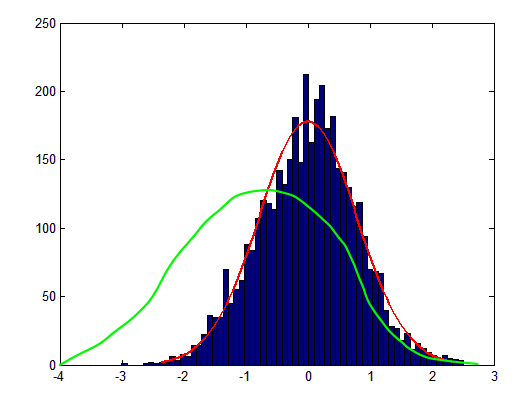
bad-distribution-fit.png

The "badness" of this fit could be determined by finding the difference between the data and the curve.

We can plot every possible parameter value on a chart.

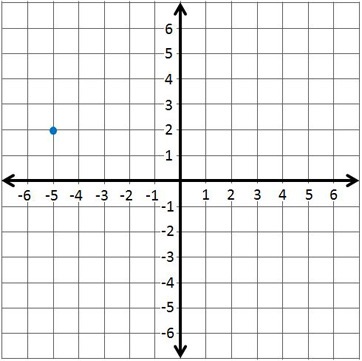
x-y-graph.jpg

Each guess could be expressed as a vector.

\begin{equation} \begin{bmatrix} \sigma \\ \mu \end{bmatrix} = \begin{bmatrix} 2 \\ -5 \end{bmatrix} \end{equation}

The total set of vectors and their "badness" (or cost) values create a contour. To get the best fit, we need to minimize the cost. Once we have a point, we need to find out where to go next. This direction is found with calculus. Each "jump" or "move" is a new vector. We need vector operations to be able to express this movement.

An example of a "badness" calculation is the Sum of Squared Residuals (SSR). Here we take all of the residuals (the difference between the measured and predicted data), square them and add them together.

TODO Matrices