Normal Distribution

The distribution's probability density function is

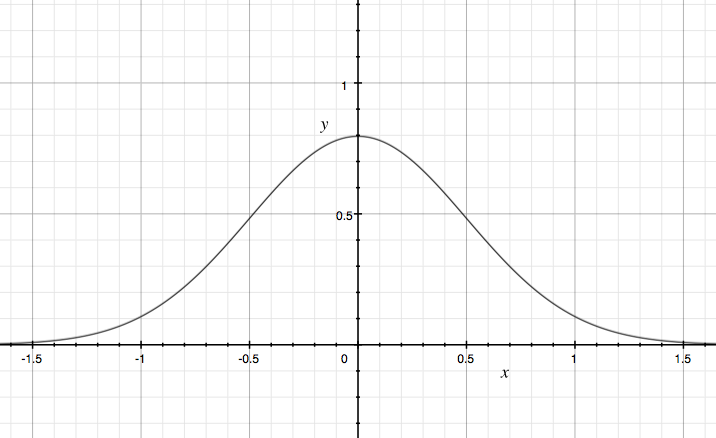
\begin{equation} f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}} \end{equation}

This equation has two parameters: \(\mu\) and \(\sigma\). \(\mu\) is the mean of the distribution. \(\sigma\) is the standard deviation. The normal distribution is often just represented by these two parameters.

• Bell-shaped curve.
• Total area under the curve is 1.
• Symmetrical

The standard normal distribution is simply when \(\mu\) = 0, \(\sigma\) = 0.