Tries

A trie is a tree data structure often used to store strings. Every leaf of the trie represents one string. Each node on the path from root to leaf is labeled with exactly one character of the string. Information on this page is taken from section 12.3 of The Algorithm Design Manual by Steven S. Skiena.

Here's a trie on strings the, their, there, was, and when.

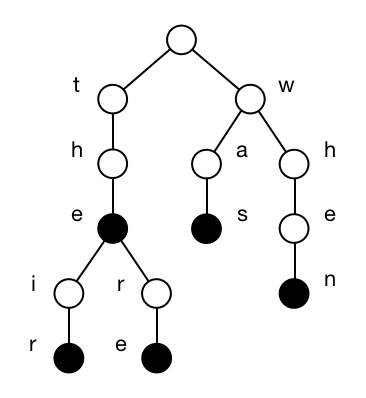
Tries are useful for testing whether a given query string q is in the set. We traverse the trie from the root along branches defined by successive characters of q. If a branch does not exist in the trie, then q cannot be in the set of strings. Otherwise we find q in |q| character comparisons regardless of how many strings are in the trie.

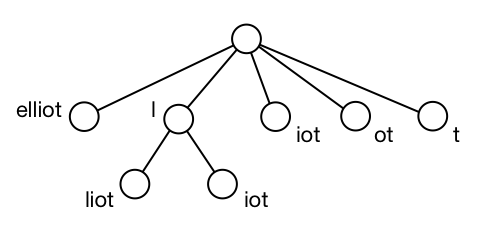
A suffix tree is a trie of all proper suffixes of \(S\). A suffix tree enables one to test whether \(q\) is a substring of \(S\), because any substring of \(S\) is a prefix of some suffix. Here's a suffix tree on elliot.

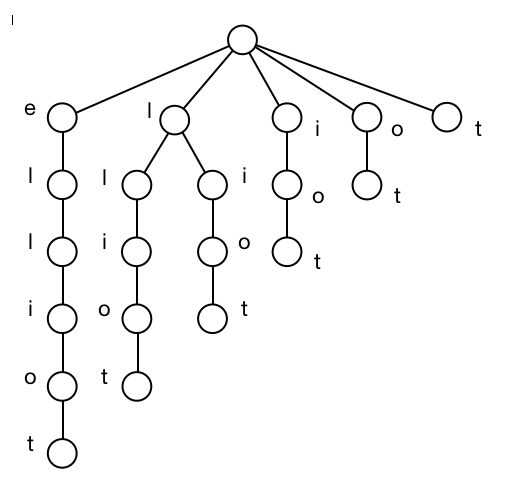
Constructed naively, a suffix tree requires \(O(n^2)\) time and space. A compressed trie, however, requires linear space. This trie is obtained by joining chains of single nodes. The nodes of a compressed trie also often store index ranges instead of actual strings. Here's a compressed suffix tree on elliot.