Genetic Algorithms
Information on this page is taken (often directly) from Wikipedia.
A genetic algorithm (GA) is a type of evolutionary algorithm (EA) often used for optimization problems. Genetic algorithms usually maintain a population of entities that possess a collection of values (the genes). Through selection, crossover, and mutation, the algorithm evolves these individuals to produce better solutions. Each candidate solution is traditionally represented as binary string of 0s and 1s, but other encodings are also possible.
The evolution usually starts from a population of randomly generated individuals, and is an iterative process, with the population in each iteration called a generation. In each generation, the fitness of every individual in the population is evaluated; the fitness is usually the value of the objective function in the optimization problem being solved. The more fit individuals are stochastically selected from the current population, and each individuals's genome is modified (recombined and possibly randomly mutated) to form a new generation.
Selection
During each successive generation, a portion of the existing population is selected to breeed a new generation. Individual solutions are selected through a fitness-based process, where fitter solutions are typically more likely to be selected. The fitness problem is always problem dependent.
In some problems, it is hard or even impossible to define the fitness expression; in these cases a simulation may be used to determine the fitness function value of a phenotype.
Fitness Proportionate Selection
The fitness function assigns a fitness to possible solutions or chromosomes. This fitness level is used to associate a probability of selection with each individual chromosome. If \(f_i\) is the fitness of individual \(i\) in the population, its probability of being selected is
\begin{equation} p_i = \frac{f_i}{\sum_{j=1}^{N} f_j} \end{equation}where \(N\) is the number of individuals in the population.
Genetic Operators
The next step is a generate a second generation population of solutions from those selected through a combination of genetic operators: crossover (also called recombination) and mutation.
It is worth tuning parameters such as the mutation probability, crossover probability, and population size to find reasonable settings for the problem class being worked on. A very small mutation rate may lead to genetic drift. A recombination rate that is too high may lead to premature convergence of the genetic algorithm. A mutation rate that is too high may lead to loss of good solutions, unless elitist selection is employed.
Crossover/Recombination
This genetic operator is analogous to reproduction. Crossover is a process of taking more than one parent solution and producing a child solution from them.
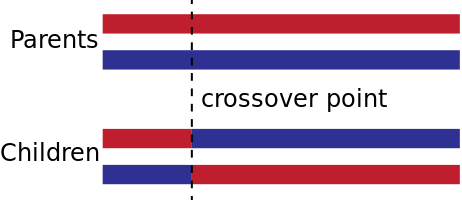
Single-Point
A single crossover point on both parents' organism strings is selected. All data beyond that point in either organism string is swapped between the two parent organisms.
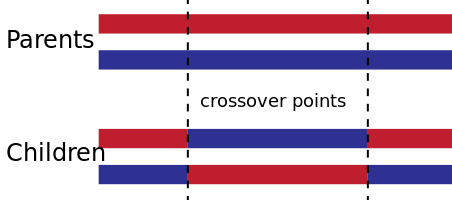
Two-Point
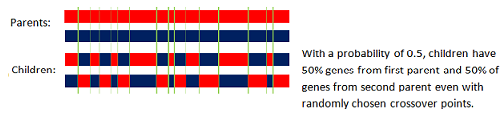
Uniform
In the uniform crossover scheme (UX) individual bits in the string are compared between two parents. The bits are swapped with a fixed probability (called recombination probability).
Mutation
This genetic operator is used to maintain genetic diversity from one generation of a population to the next. It is analogous to biological mutation. Mutation alters one or more gene values in a chromosome from its initial state. Mutation occurs during evolution according to a user-definable mutation probability. This probability should be set low. If it is set too high, the search will turn into a primitive random search.
Mutation should allow the algorithm to avoid local minima by preventing the population of chromosomes from becoming too similar to each other, thus slowing or even stopping evolution. This reasoning also explains the fact that most GA systems avoid only taking the fittest of the population in generating the next but rather a random selection with a weighting toward those that are fitter.
Bit String Mutation
The mutation of bit strings ensue through bit flips at random positions. The probability of a mutation of a bit is \(1/l\) where \(l\) is the length of the binary vector.
Gaussian
This operator adds a unit Gaussian distributed random value to the chosen gene (potentially all genes). Each vector component \(x_i\) becomes
\begin{equation} x'_i = x_i + N_i(0,\sigma_i) \end{equation}Where \(N_i(0,\sigma)\) is a normally distributed random number with mean 0 and standard deviation \(\sigma_i\). All \(N_i\) are generated independently.
Chromosome Representation
The simplest algorithm represents each chromosome as a bit string. Arrays of floating point numbers have also been used.
Elitism
A practical variant of the general process of constructing a new population is to allow the best organism(s) from the current generation to carry over to the next, unaltered. This strategy is known as elisit selection and guarantees that the solution quality obtained by the GA will not decrease one generation to the next.