Context Free Grammars
A context-free grammar (CFG) is a precise description of language syntax. Each rule or production of the grammar defines an interpretation for the named symbol on the left side of the rule as a sequence of symbols on the right side of the rule. The right side can be a combination of nonterminals (themselves defined by rules) or terminal symbols defined simply as strings, such as "the", "a", "cat", "milk", and "drank".
Parsing a text string \(S\) according to a given context-free grammar \(G\) is the algorithm problem of constructing a parse tree of rule substitutions defining \(S\) as a single nonterminal symbol of \(G\). One of the nonterminals, usually the one on the left-hand side of the first production, is called the start symbol. It names the construct defined by the overall grammar.
Example
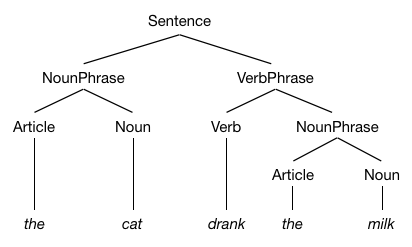
Sentence ::= NounPhrase VerbPhrase NounPhrase ::= Article Noun VerbPhrase ::= Verb NounPhrase Article ::= the, a Noun ::= cat, milk Verb ::= drank
Chomsky Normal Form
Chomsky normal form (CNF) requires the right side of every rule to consist of
- exactly two nonterminals, i.e. \(X -> YZ\), or
- exactly one terminal symbol, i.e. \(X -> \alpha\).
Any context-free grammar can be easily and mechanically transformed into Chomsky normal form by repeatedly shortening long right-hand sides at the cost of adding extra nonterminals and productions. Thus, there is no loss of generality with this assumption.
Bottom-Up Parsing
The CYK algorithm efficiently parses a string using dynamic programming. The algorithm only works on grammars in Chomsky normal form. This section is taken from The Algorithm Design Manual by Steven S. Skiena.
Define \(M[i, j, X]\) to be a boolean function that is true iff substring \(S[i, j]\) is generated by nonterminal \(X\). This is true if there exists a production \(X -> YZ\) and breaking point \(k\) between \(i\) and \(j\) such that the left part generates \(Y\) and the right part \(Z\). In other words,
\begin{equation} M[i, j, X] = \bigvee\limits_{(X -> YZ) \in G} \Big( \bigvee\limits_{k=i}^j M[i, k, Y] \wedge M[k + 1, j, Z] \Big) \end{equation}Where \(\vee\) denotes the logical or over all productions and split positions, and \(\wedge\) denotes the logical and of two boolean values.
The one-character terminal symbols define the boundary conditions of the recurrence. In particular, \(M[i, i, X]\) is true iff there exists a production \(X -> \alpha\) such that \(S[i] = \alpha\).
TODO Example
TODO Implementation
TODO Top-Down Parsing
TODO: LL parser, LL(1)