Fractals

Something is regarded as a fractal if all or most of the following properties hold in some form.

• Fine structure
  • Irregularities at arbitrarily small scales. This is very different from, say, a circle where a small portion of the perimeter sufficiently magnified will appear almost indistinguishable from a straight line.
• Self-similarity
  • Made up of smaller scale copies of itself. See the section on self-similarity below.
• Classical mathematics are not applicable
  • Traditional Euclidean geometric language doesn't easily describe fractals. Fractals often have infinite length and zero area.
• Recursive definition
  • Many fractals are constructed by performing a simple step over and over again.

The definition of a fractal is somewhat analogous to the way biologists define 'life'. Something is held to be alive if it has all or most of the characteristics on a list: ability to grow, ability to reproduce, ability to respond to stimuli in some way, etc.

Take a straight line (\(E_0\)) and divide it into three equal pieces. Erase the middle piece, and replace this by the other two sides of an equilateral triangle on the same base (\(E_1\)). Repeat with each of these four pieces (\(E_2\)).

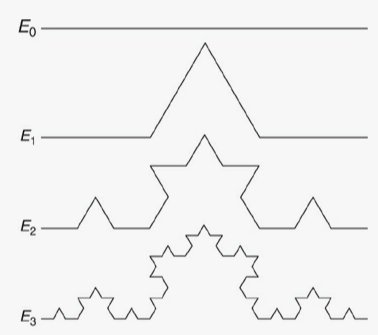
Repeated indefinitely, this procedure becomes the von Koch curve (\(F\)).

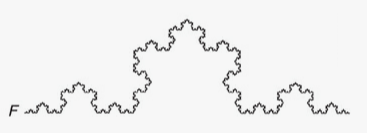
This fractal was introduced and studied by the Swedish mathematician Helge von Koch in 1906. This fractal displays fine structure as a consequence of being self-similar: the curve consists of four parts, each a 1/3 scale copy of the entire curve.

If we take three copies of the von Koch curve and join them corner to corner in a triangle, we get the von Koch snowflake.

Fractals are often drawn on a plane with a collection of points. This collection of points is referred to as a set. A set might be a circle, a von Koch curve, or the silhouette of a person.

A set can be formed by repeatedly applying a function. Given a function (e.g. \((x, y) -> (x + 1, y)\)) and some initial point, we discover a new point. Applying the function to this point gives us a third point. The process of repeatedly applying the function is known as iterating the function and the points visited are the iterates of the initial point. Iterates jump around and build up a curved, stratified figure called the attractor of the function.

Repeated application of a simple operation may give rise to a complex, fractal form. A fractal attractor is sometimes called a strange attractor.

Two figures are similar if they have the same shape, but not necessarily the same size. Objects are congruent if they have the same shape and size. A self-similar set is one that is made up of several smaller similar copies of itself.

The Koch curve is self-similar since it comprises 4 suitably placed scale \(1/3\) copies of itself. This may be represented diagrammatically by a template consisting of one large rectangle and 4 smaller ones, each a \(1/3\) copy of the large one.

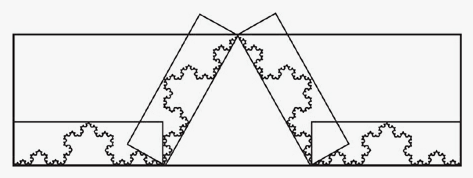
Put generally, a template consists of some simple shape (square, rectangle, triangle, etc.) and a number of smaller similar copies of the shape positioned somehow in the plane. Each of the smaller shapes represents a transformation that scales and repositions the larger shape. The template completely defines the fractal: given a template, there is essentially just one figure, usually a fractal, that is made up of smaller scaled copies of itself positioned as indicated.

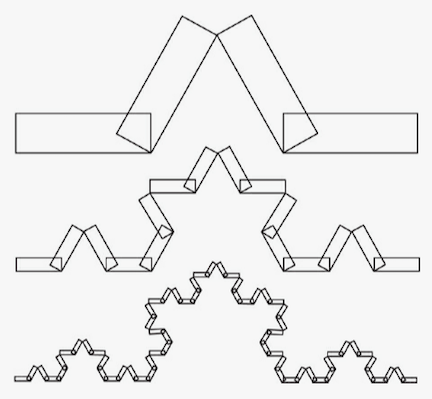
There are 8 different similarities that transform a square to a smaller square. The scaling can be direct or there can be a rotation through 90°, 180°, or 270°, or a mirror reflection in a vertical, horizontal, or one of the two diagonal lines. We refer to these possibilities as the orientations of the scalings. The orientations of the similarity transformations must be specified to remove ambiguity.

Templates are simply a diagrammatic way of expressing a family of transformations or functions. Each of the smaller shapes codes the similarity transformation which takes the large shape and scales it down to the size and position of the smaller one. The functions have the advantage that they also encode the orientations of the transformations. The Chaos Game is a method of constructing templates with functions.

1. Take any initial starting point.
2. Select one of the functions at random.
3. Apply the chosen function to get the next point.
4. Go to step 2.

An affine transformation is more general than a similarity, in that it scales by different ratios in different directions and so elongates objects. For example, affine transformations transform squares into rectangles or parallelograms, and circles into ellipses. A self-affine fractal is one that is made up of smaller affine copies of itself.

The (right angled) Sierpinski triangle is made up of 3 copies of itself at scale \(1/2\).

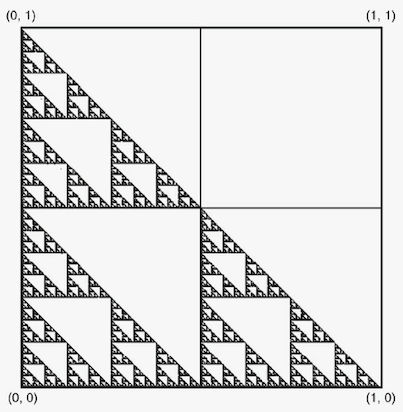
The three functions giving the three similarity transformations that transform the unit square to the bottom left, bottom right, and top left squares respectively, have the formulae:

\begin{equation} (x, y) \rightarrow (\frac{1}{2}x,\frac{1}{2}y) \end{equation} \begin{equation} (x, y) \rightarrow (\frac{1}{2}x + \frac{1}{2},\frac{1}{2}y) \end{equation} \begin{equation} (x, y) \rightarrow (\frac{1}{2}x,\frac{1}{2}y + \frac{1}{2}) \end{equation}

The traditional Sierpinski triangle is constructed with equilateral triangles.