Naked Statistics by Charles Wheelan

A descriptive statistic is a summary of raw data that makes the underlying phenomenon meaningful and manageable. Be careful! Any simplification invites abuse.

Mean (\(\mu\)) and median are descriptive statistics. While outliers can greatly affect the mean, the median usually ignores them. Quertiles are divisions of the distribution into quarters (first quartile is the bottom 25 percent of observations, etc). Each percentile represents 1 percent of the distribution.

An absolute score, number, or figure has some intrinsic meaning. A relative value has meaning only in comparison to something else. For example, 43/60 on an exam is an absolute score, the 8th percentile is a relative score.

The standard deviation (\(\sigma\)) is a measure of how dispersed the data are from their mean. For many typical distributions of data, a high proportion of the observations lie within one standard deviation of the mean.

Data that are distributed normally are symmetrical around their mean in a bell shape. By definition of the normal distribution, 68.2 percent of observations lie within one standard deviation of the mean, 95.4 percent lie within two standard deviations of the mean.

An index is a descriptive statistic made up of other descriptive statistics. An index is highly sensitive to its parts and their weights.

Although the field of statistics is rooted in mathematics, and mathematics is exact, the use of statistics to describe complex phenomena is not exact. A crucial distinction exists between precision and accuracy. Precision reflects the exactitude with which we can express something. Accuracy is a measure of whether a figure is broadly consistent with the truth. If an answer is accurate, then more precision is usually better. But no amount of precision can make up for inaccuracy.

Deception can come from a variety of places. Always check measurements or calculations against common sense!

• Sometimes you need more than one descriptive statistic to understand the data.
• Pay attention to the unit of analysis. Who or what is being described? Cell phone coverage by land area might be different than coverage by person.
• The mean is sensitive to outliers, while the median is not. Do outliers distort the description or are they an important part of the message?
• Don't compare "apples and oranges." For example, both exchange rates and inflation can affect money comparisons. Normal figures are not adjusted for inflation but real figures are.
• Percentages can be used to exaggerate. Percentage will be high for a very low starting point. On the flip side, a small percentage of an enormous sum can be a big number.
• Any comparison over time must have a start point and an end point. One can sometimes manipulate those points in ways that affect the message.

Correlation measures the degree to which two phenomena are related to one another. Two variables are positively correlated if a change in one is associated with a change in the other in the same direction. A correlation is negative if a positive change in one variable is associated with a negative change in the other. Note that not every observation has to fit the pattern for variables to be correlated.

We can encapsulate an association between two variables in a single descriptive statistic: the correlation coefficient. The correlation coefficient is a single number ranging from -1 to 1 with no units attached. A correlation of 1, often described as perfect correlation, means that every change in one variable is associated with an equivalent change in the other variable in the same direction. A correlation of -1, or perfect negative correlation, means that a change in one variable is associated with an equivalent change in the other variable in the opposite direction.

The correlation coefficient is calculated by finding the distance (in standard deviations) from the mean for each observation. The equation then finds the relationship between the variables using these standard units.

\begin{equation} r = \frac{1}{n} \sum_{i=1}^{n} \frac{(x_i - \bar{x})}{\sigma_x} \frac{(y_i - \bar{y})}{\sigma_y} \end{equation}

Probability is the study of events and outcomes involving an element of uncertainty. Many events have known probabilities. The probability of flipping heads with a fair coin is \(\frac{1}{2}\). Other events have probabilities that can be inferred on the basis of past data. Probabilities do not tell us what will happen for sure; they tell us what is likely to happen and what is less likely to happen. Probability can also sometimes tell us after the fact what likely happened and what likely did not happen.

The probability of two independent events both happening is the product of their respective probabilities. If the probability of flipping heads with a fair coin is \(\frac{1}{2}\), then the probability of flipping heads twice in a row is \(\frac{1}{2} \times \frac{1}{2}\), or \(\frac{1}{4}\). This is only the case if the events are independent. The probability that it rains today is not independent of whether it rained yesterday, since storm fronts can last for days.

If the events are mutually exclusive, such as throwing a 1, 2, or 3 with a single die, the probability of getting A or B consists of the sum of their individual probabilities. If the events are not mutually exclusive, such as drawing a five or a hears from a deck of cards (5 of hearts fits both groups), the probability of getting A or B consists of the sum of their individual probabilities minus the probability of both events happening.

The expected value is the sum of all the different outcomes, each weighted by its probability and payoff. Let's say we a dice game where the payoff is $1 if you roll a 1; $2 if you roll a 2, etc. Each possible outcome has a \(\frac{1}{6}\) probability, so the expected value is

\begin{equation} \frac{1}{6}($1) + \frac{1}{6}($2) + \frac{1}{6}($3) + \frac{1}{6}($4) + \frac{1}{6}($5) + \frac{1}{6}($6) = $3.50. \end{equation}

The law of large numbers tells us that as the number of independent trials increases, the average of the outcomes will get closer and closer to its expected value. A probability density function plots the assorted outcomes along the x-axis and the expected probability of each outcome on the y-axis; the weighted probabilities - each outcome multiplied by its expected frequency - will add up to 1. With more trials, the plot will become skinnier and skinnier.

A decision tree maps out each source of uncertainty and the probabilities associated with all possible outcomes. The end of the tree gives us all the possible payoffs and the probability of each.

Prior to the 2008 financial crisis, firms throughout the financial industry used a common barometer of risk, the Value at Risk model, or VaR. VaR had two catastrophic problems. Firstly, the underlying probabilities on which the models were built were based on past market movements; however, in financial markets, the future does not necessarily look like the past. Secondly, the "tail risk" and their true potential damage was neglected. Unlikely things happen. In fact, over a long enough period of time, they are not even that unlikely.

Here are some of the most common probability-related errors:

• Assuming events are independent when they are not.
• Not understanding when events are independent.
  • e.g. people looking at the dice and declaring that they are "due."
• Clusters happen.
  • If a log of people flip coins, someone will get a streak.
• The prosecutor's fallacy.
  • This fallacy occurs when the context surrounding statistical evidence is neglected. For example, if you look for a one in a million DNA match if you run through a database of a random million people.
• Reversion to the mean (or regression to the mean).
  • Probability tells us that any outlier is likely to be followed by outcomes that are more consistent with the long-term average.

Good data are essential. No amount of fancy analysis can make up for fundamentally flawed data: garbage in, garbage out.

The data sample needs to be representative of some larger group or population. Sampling is the process of gathering data for a small area and then using those data to make an informed judgment, or inference, about the population as a whole. Sampling requires far less resources than trying to count an entire population; done properly, it can be every bit as accurate. The easiest way to gather a representative sample of a larger population is to select some subset of that population randomly (known as a simple random sample).

Data should provide some source of comparison. Is a new medicine more effective than the current treatment? We do this to isolate the impact of one specific intervention of attribute. Researchers usually try to create a control group and a treatment group. Ideally, one would randomly assign to these groups.

Bad data can appear for many reasons.

• Selection bias: If you ask 100 people in a public place to complete a short survey, and 60 are willing to answer your questions, those 60 are likely to be different in significant ways from the 40 who walked by without making eye contact.
• Publication bias appears because positive findings are more likely to be published than negative findings.
• Recall bias can appear because memory is not always a good source of data. Recall bias is one reason that longitudinal studies are often preferred to cross-sectional studies.
• Survivorship bias occurs when some or many of the observations are falling out of the sample. For example, the average test scores of students in high school will rise steadily for four years. But…each year some of the students drop out!

The central limit theorem tells us that a large, properly drawn sample will resemble the population from which it is drawn. There will be variation from sample to sample, but the probability that any sample will deviate massively from the underlying population is very low.

• If we have detailed information about some population, then we can make powerful inferences about any properly drawn sample from that population.
• Conversely, if we have detailed information about a properly drawn sample, we can make strikingly accurate inferences about the population from which the sample was drawn.
• We can calculate the probability that a particular sample was drawn from a given population.
• We can infer whether or not two samples were likely drawn from the same population.

According to the central limit theorem, the /sample means for any population will be distributed roughly as a normal distribution around the population mean/. The will be true no matter what the distribution of the underlying population looks like.

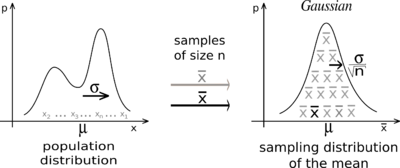
The standard error measures the dispersion of the sample means (it's the standard deviation). Here's the equation for standard error:

\begin{equation} SE = \frac{s}{\sqrt{n}} \end{equation}

Where \(s\) is the standard deviation of the population from which the sample is drawn, and \(n\) is the size of the sample. The standard error grows when the population is more diverse and shrinks when the sample size increases. For large samples, we can assume that the standard deviation of the sample is reasonably close to the standard deviation of the population.

Statistics cannot prove anything with certainty. Inference tells us what is likely, and what is unlikely. Any statistical inference begins with an implicit or explicit null hypothesis. This is our starting assumption, which will be rejected or not on the basis of subsequent statistical analysis. If we reject the null hypothesis, then we typically accept some alternative hypothesis. The null hypothesis and alternative hypothesis are logical complements. If one is true, the other is false. Researchers often create a null hypothesis in hopes of being able to reject it.

One of the most common thresholds that researchers use for rejecting a null hypothesis is 5 percent or 0.05. This probability is known as a significance level, and it represents the upper bound for the likelihood of observing some pattern of data if the null hypothesis were true. The p-value is the specific probability of getting the result you've observed if the null hypothesis is true. When we can reject a null hypothesis at some reasonable significance level, the results are said to be statistically significant. If there is "no statistically significant association" between two variables then the relationship between the two variables can reasonably be explained by chance alone.

Often we're comparing two samples to see if they come from the same population. Suppose your null hypothesis is that male professional basketball players have the same mean height as the rest of the adult male population. You randomly select 37 basketball players (all professionals that would come!) and 50 average men. The means are 6'7" and 5'10". You find that the standard error of these groups is around 0.8 and 0.4. You can build a confidence interval that stretches two standard errors: \(6'7"\pm1.6\) and \(5'10"\pm0.8\). The lower bound of our 95 percent confidence interval of basketball players is still higher than the upper bound for the 95 confidence interval for average men. Since our confidence intervals do not overlap, these samples likely do not come from the same population and we can reject the null hypothesis.

A Type I error involves wrongly rejecting the null hypothesis (a false positive). A Type II error involves failing to reject a false null hypothesis (a false negative). Let's say that we are building a spam filter. The null hypothesis is that any particular e-mail message is not spam. A Type I error would involve screening out an e-mail message that is not actually spam. A Type II error would involve letting spam through the filter into your inbox. What kind of error is worse depends on the circumstances. In this example, people would probably err on the side of allowing Type II errors. Significance level will affect how much you see one type of error vs. the other type of error.

A poll (or survey) is an inference about the opinions of some population that is based on the views expressed by some sample. The central limit theorem tells us that a large, representative sample will look a lot like the population from which it is drawn.

In a poll, the sample statistic we care about is not a mean but rather a percentage or proportion. For any properly drawn random sample, the standard error is equal to

\begin{equation} \sqrt{\frac{p(1 - p)}{n}} \end{equation}

Where \(p\) is the proportion of respondents expressing a particular view, \((1 - p)\) is the proportion of respondents expressing a different view, and \(n\) is the total number of respondents in the sample. This standard error will be small when the sample size is large or when \(p\) and \((1 - p)\) are far apart.

When polling, use accurate samples, ask good questions, and ensure respondents are telling the truth. Avoid self-selection and be aware of response rate. Note that different phrases ("tax relief" vs. "tax cuts" and "climate change" vs. global words") can elicit different responses.

Regression analysis allows us to quantify the relationship between a particular variable and an outcome that we care about while controlling for other factors. The hard part in regression analysis is determining which variables ought to be considered in the analysis.

At its core, regression analysis seeks to find the "best fit" for a linear relationship between two variables. Typically we use ordinary least squares (OLS). OLS fits the line that minimizes the sum of the squared residuals.

Regression analysis outputs an equation that describes a line: \(y = a + bx\). The variable that is being explained is known as the dependent variable (\(y\)). The variables that we are using to explain our dependent variable are explanatory variables (or independent variables). The slope of the line (\(b\)) is the regression coefficient.

For any regression coefficient, you will be interested in sign, size, and significance. To determine if the coefficient is significant, we can use standard error and test the null hypothesis. Note that the formula for calculating the standard error for a coefficient was purposely avoided in Naked Statistics.

Regression analysis also produces \(R^2\). This statistic is a measure of the total amount of variation explained by the regression equation. An \(R^2\) of zero means that our regression equation does no better than the mean. An \(R^2\) of 1 means that the regression equation perfectly predicts elements in the sample. A value below one means that some variation still needs explanation.

Multivariate regression (or multiple regression) is regression analysis with multiple explanatory variables. This type of regression will give us a coefficient for each explanatory variable included in the regression equation. These coefficients estimate the linear association between each explanatory variable and the dependent variable while holding other dependent variables constant. Multivariate regression thus lets us quantity a relationship while controlling for other variables. It's the best tool for finding meaningful patterns in large, complex data sets.

• Using regression to analyze a nonlinear relationship.
• Assuming that correlation equals causation.
• Not considering reverse causality (B might cause A instead of A causing B).
• Omitting variables.
  • Regression results will be misleading and inaccurate if the regression equation leaves out an important explanatory variable, particularly if other variables in the equation "pick up" that affect.
  • For example, suppose we explain test scores by school spending alone. We're probably omitting parental education (among other variables). Well-educated families tend to live in affluent areas that spend a lot of money on their schools. Our school spending explanatory variable would probably pick up the parent education level variable.
• Using highly correlated explanatory variables (multicollinearity).
• Extrapolating beyond the data.
• Data mining (using too many variables).

Program evaluation is the process by which we seek to measure the causal effect of some intervention. The intervention that we care about is typically called the treatment (though that term is overloaded). We are seeking to isolate the effect of that single factor; ideally we would like to know how the group receiving that treatment fares compared with some other group whose members are identical in all other respects but for the treatment.

Program evaluation offers a set of tools for isolating the treatment effect when cause and effect are otherwise elusive.

• Randomized, controlled experiments.
  • The most straightforward way to create a treatment and control group is in an experimental setting, though this isn't always possible.
  • The optimal way to create the two groups is to distribute the study participants randomly across the two groups. The randomization will generally distribute the non-treatment-related variables more or less evenly between the two groups.
• Natural experiment.
  • Sometimes the treatment and control group are created by accident. Perhaps by different laws or unique practices.
• Nonequivalent control.
  • Sometimes the best available option for studying a treatment effect is to create non-randomized treatment and control. This creates a bias, but we might be able to cleverly remote it.
• Difference in differences.
  • One of the best ways to observe cause and effect is to do something and see what happens!
  • We compare the "before" and "after" data for a group that received the treatment to the "before" and "after" data for a similar group that didn't receive the treatment.
• Discontinuity analysis.
  • Here we compare the outcomes for some group that barely qualified for an intervention or treatment with the outcomes for a group that just missed the cutoff for eligibility and did not receive the treatment.